Algorithmic cheatsheet
2014-10-02
This page sums up some important results from computer science. They are extracted from the Introduction to Algorithms (Third Edition), by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein. We highly recommend it.
The following information is organized in several sections grouping definitions. Each definition points to the Introduction to Algorithms for further information using the abbreviation CLRS (from the authors’ names).
The formulæ are written using \(\LaTeX\) and the final render of the page is done by the Javascript library MathJax (currently the simplest way to use \(\LaTeX\) in HTML).
The current figures use images from external websites. Clicking on it will redirect you to their original webpages.
General results
Master Theorem
CLRS: p93
Recurrence of the form: \(T(n) = a T(n/b) + O(f(n))\)
| Case | \(f(n) = O(\dots)\) | \(T(n) = O(\dots)\) |
|---|---|---|
| 1 | \(n^{\log_b a - \varepsilon}\) | \(n^{\log_b a}\) |
| 2 | \(n^{\log_b a}\) | \(\log n \times n^{\log_b a}\) |
| 3 | \(n^{\log_b a + \varepsilon}\) and \(\exists c, a f(n/b) \leq c f(n)\) | \(f(n)\) |
http://anupcowkur.com/posts/master-theorem-simplified/ http://www.geeksforgeeks.org/analysis-algorithm-set-4-master-method-solving-recurrences/ http://rosalind.info/glossary/algo-master-theorem/
call tree; \(b\) defines the maximal depth of the recursive calls, \(a\) defines the maximal number of calls to \(f\) at each level, summing the complexity of each of the \(O(n^{\log_b a})\) calls to \(f\), which depends on the depth, explains the cases of the master theorem (the illustraction come from the CLRS Second Edition)
Matroid
CLRS: p437
Pair \((S, \mathcal I)\) with:
- \(S\) is a finite set
- \(\emptyset \neq \mathcal I \subseteq \mathcal P(S)\) (independent subsets)
- \(\forall A \subseteq B \in \mathcal I, A \in \mathcal I\) (heredity)
- \(\forall A,B \in \mathcal I, |A| \lt |B| \Rightarrow \exists x \in B \backslash A, A \cup \{x\} \in \mathcal I\)(exchange)
Greedy algorithms from matroids
CLRS: p439
\((S, \mathcal I)\) is a matroid. \(w\) is a weight function over \(S\). Greedy algorithm → choosing iteratively an element maximizing \(w\):
- \(\{x\} \in \mathcal I\) with maximum weight
- \(x\) is in any independent subset with maximum weight
- \(\mathcal I' = \{B \subseteq S \backslash \{x\} : B \cup \{x\} \in \mathcal I\}\) (subsets containing \(x\), ignoring \(x\))
- \(S' = \{y \in S, \{x,y\} \in \mathcal I)\) (restricting elements)
- iterate on \((S', \mathcal I')\) (also a matroid)
Data structures
Heap
CLRS: p151
Sorted data structure (priority queue) Min-heap: parent is bigger than its children Max-heap: parent is bigger than its children
| Operation | Complexity |
|---|---|
| Memory use | \(O(n)\) |
| Insert | \(O(\log n)\) |
| Maximum | \(O(1)\) |
| Extract-Max | \(O(\log n)\) |
| Increase-Key | \(O(\log n)\) |
Hash Table
CLRS: p256
Arbitrarily indexed table \(h\) is a hash function to \([1..m]\)
- Space: \(O(m)\)
- Locate: \(O(1 + n/m)\)
Note: Locate finds a location in the array where the user can read or write as usual.
Binary Search Tree (BST)
CLRS: p286
Sorted data structure \(h\) is the height of the tree
- Space: \(O(n)\)
- Search: \(O(h)\)
- Insert: \(O(h)\)
- Delete: \(O(h)\)
Red-Black Tree
CLRS: p308
BST maintaining \(h = \log n\) with:
- every node is either black (“normal”) or red (to be updated);
- the root is black;
- leaves are black;
- red nodes cannot have a red parent → there are no more red nodes than black ones;
- all simple paths from the root to a leaf have the same number of black nodes, limiting \(h\).
B-Tree
CLRS: p484
Variant of the BST using a large fan-out \(t\) to reduce disk-accesses Search, insert and delete take \(O(\log_t n)\) disk accesses and \(O(t \log_t n)\) CPU time.
Union-find
CLRS: p568
Data structure for sets, supporting union of sets and finding the representative \(m\) is the number of previously run Make-Set operations. \(\alpha\) is the Ackerman function (\(\alpha(m) \leq 4\) in practise).
- Make-Set: \(O(1)\)
- Union: \(O(1)\)
- Find-Set: \(O(\alpha(m))\)
http://scienceblogs.com/goodmath/2007/09/06/graph-searches-and-disjoint-se/
Sorting
Bubblesort
CLRS: p40 (problem 2-2) Complexity: \(O(n^2)\)
Fixing inverted adjacent values \(n\) times
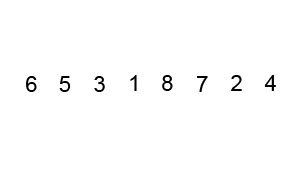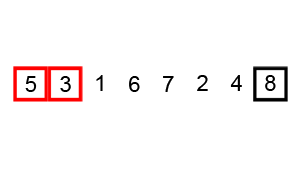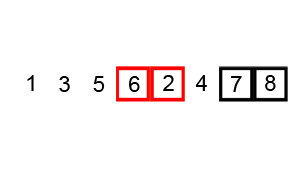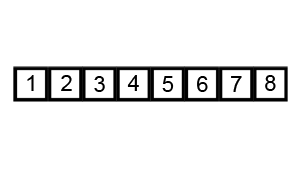
Insertion sort
CLRS: p16 (correctness), p24 (complexity) Complexity: \(O(n^2)\)
Inserting each element in a new array at the right location
Merge sort
CLRS: p29 Complexity: \(O(n \log n)\)
Divide-and-conquer (sort each half, then merge)
Heapsort
CLRS: p159 Complexity: \(O(n \log n)\)
Building a heap on the \(n\) elements and extracting them all
Quicksort
CLRS: p170 Complexity: \(O(n \log n)\)
Divide-and-conquer (choose a pivot, then filter lower and greater values)
Graph algorithms
{Breadth,Depth}-first search
CLRS: p594 (breadth), p603 (depth) Complexity: \(O(E + V)\)
Listing the vertices of a graph. Breadth-first search list the siblings, then the siblings’ siblings…
Depth-first search goes as far as it can before considering siblings.
Kruskal
CLRS: p631 Complexity: \(O(E \log V)\)
Finding a minimum spanning tree Consider every edge in nondecreasing order, add to current forest if links two components. The components are handled using union-find.
Prim
CLRS: p634 Complexity: \(O(E \log V)\) (binary heap) Complexity: \(O(E + V \log V)\) (Fibonacci heap)
Finding a minimum spanning tree Iteratively extract closest vertex \(u\) and relax all edges \((u, v)\). The set of vertices is handled using a priority queue.
Bellman-Ford
CLRS: p651 Complexity: \(O(E V)\)
Finding all shortest paths from a single source Just relax every edge of the graph |V| times Detects negative weight cycles
Shortest paths from DAG
CLRS: p655 Complexity: \(O(V+E)\) (including sorting)
Finding all shortest paths from a single source in Directed Acyclic Graphs Consider every vertex \(u\) in topological order and relax all edges \((u, v)\)
Dijkstra
CLRS: p658 Complexity: \(O(V^2 + E)\) (array) Complexity: \(O((E+V) \log V)\) (binary heap) Complexity: \(O(V \log V + E)\) (Fibonacci heap)
Finding all shortest paths from a single source with positive weights Iteratively extract closest vertex \(u\) and relax all edges \((u, v)\). The set of vertices is handled using a priority queue.
Floyd-Warshall
CLRS: p693 Complexity: \(O(V^3)\)
Finding the shortest path from all vertex pairs Relaxing pair distance \(|V|\) times